Numerical Simulation of Detonations

Daniel Neale Williams
Department of Mechanical Engineering
The University of Calgary
Calgary, Alberta, CANADA
dnwillia@acs.ucalgary.ca

This will be changing from time to time. As I work on it when I get a chance.

The results are divided into three different sections as follows:

One-Dimensional Results
Two-Dimensional Results
Three-Dimensional Results
Numerical Smoke Foils

Detonations are the most violent form of combustion. A detonation consists of a shock wave that propagates into a combustible mixture that raises the temperature of that mixture enough for burning to take place. Detonations typically propagate at many times the speed of sound and can be extremely destructive as a result.

One of the classical motivations for studying detonations is the problem of deflagration to detonation transition (DDT). This is where a slow, ordinary flame, which propagates on the order of 10-100 m/s turns into a detonation that propagates at 2000-3000 m/s (At least in that order of magnitude). The ability to accurately predict this process is of great interest to many researchers; however, the computational study of the process is still not feasible with current computer technology. So then, why do we still study this phenomenon? Well, if we ever hope to fully understand DDT, it is also important to understand the underlying physics of detonation propagation. If we can do this properly in the present, then we should eventually be able to do DDT right as well.

DDT is directly related to the problem of fuel-air explosions. The risk of fuel air explosions is important in connection with the transport and storage of liquid and gaseous petroluem products. In addition, there has been the question of the possibility of a hydrogen-air explosion occuring inside a nuclear reactor containment vessel. The consequences of such an explosion would be catastrophic.

It may be true that only experiments will reveal the ultimate truth of what is going on. However, there are several problems with doing experimental work with detonations that makes numerical simulation an attractive alternative. The experiments can be very costly and also dangerous to a certian extent. In addition, since the length and time scales associated with a detonation are so short, it is hard for experiments to reveal the detailed behaviour of a detonation. Numerical models at least allow us to study, in detail, the behaviour of a detonation over the short time and length scales involved.

Experimental results have largely been obtained using what are called "smoked foils". Smoked foils are created when a foil or mylar sheet, coated with soot, is inserted inside a detonation tube. When the detonation passes through the tube it etches tracks into the soot. Some examples of the results of this technique are shown in figure 1.

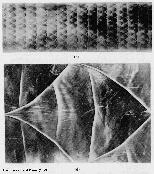
Figure 1: Some experimental smoked foils. The pictures were scanned from Fickett and Davis (1979). The experiments were performed by Strehlow (1969) which is where Fickett and Davis also obtained the pictures.

The physical model I have used is based on the Euler equations of gasdynamics with single-step chemistry goverened by Arrhenius kinetics. The equations include conservation of mass, momentum, energy and speicies, coupled by the thermal and caloric equations of state:

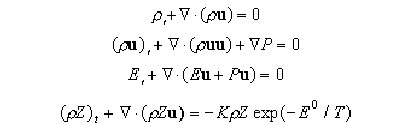
While this physical model works well for at least studying the qualitative aspects of detonation propagation, it does not hold well when one wants to determine quantitative values of interest from an engineering standpoint. In order to accurately determine parameters such as the cell size, critical tube diameters, critical initiation energy, or the hydrodynamic thickness. More complex kinetic models and the inclusion of transport effects would be necessary.

For the results shown here the detonations are characterized by four parameters. First there is the amount of overdrive f, which is the sqaure of the fraction that the detonation velocity exceeds the Chapman-Jouguet (C-J) velocity (The C-J velocity is the minimum propagation velocity of a detonation in the mixture) . Second there are the chemical parameters: the heat release Q, and the activation energy E. The parameters are all dimensionless with respect to the fixed preshock state.

The results are divided into three different sections as follows:

One-Dimensional Results
Two-Dimensional Results
Three-Dimensional Results
Numerical Smoke Foils

You are visitory number:

This page was last modified on: March 26, 1996.

Back to my homepage.